【统计学习系列】多元线性回归模型(五) |
您所在的位置:网站首页 › t检验 显著 › 【统计学习系列】多元线性回归模型(五) |
【统计学习系列】多元线性回归模型(五)
|
文章目录
1. 前文回顾2. 单参数显著性检验——t检验2.1 问题的提出2.2 检验统计量——t统计量的构造2.3 拒绝域的构造2.4 浅谈p值
3. 回归方程显著性检验——F检验3.1 问题的提出3.2 F检验统计量的构造3.3 拒绝域的构造
4. 总结参考文献写在最后
【更新日志】 5/1/2020 对文章中公式与措辞中存在的问题进行修正(感谢评论区小伙伴的指正!) 1. 前文回顾在上一篇文章中,我们分别研究了最小二乘估计量 β^OLS 和 σ^OLS 的相关性质,证明了 β^OLS 是 β 的一个最优线性无偏估计量(BLUE), σ^2OLS 是 σ2 的一个无偏估计量,并得到了其在正态性误差假设下所对应的分布: β ^ O L S ∼ N ( β , σ 2 ( X T X ) − 1 ) \bm{\hat\beta}_{OLS} \thicksim N(\bm\beta, \sigma^2 ( \bm{X}^T \bm{X} )^{-1} ) β^OLS∼N(β,σ2(XTX)−1) σ ^ O L S 2 σ 2 ∼ χ N − p − 1 2 \frac {\hat \sigma _{OLS}^2} {\sigma^2} \thicksim \chi^2_{N-p-1} σ2σ^OLS2∼χN−p−12 (详情请见:【统计学习系列】多元线性回归模型(三)——参数估计量的性质)。 通过最小二乘法拟合好模型的参数后,一个重要的问题就是:这个模型真的“好"吗?满足什么条件、什么性质的模型可以称作一个“好模型”呢? 2. 单参数显著性检验——t检验 2.1 问题的提出首先,我们应该想到的问题是,在一个多元回归模型中,是不是每一个引入的自变量对因变量都有实实在在的影响呢?这样的影响是显著的吗?我们应不应该在模型中保留这一变量呢? 在回答这些问题之前,我们先回顾一下总体模型: Y = β 0 + ∑ i = 1 p X i β i + ϵ Y= \beta_0 + \sum_{i=1}^{p} X_{i} \beta_i + \epsilon Y=β0+i=1∑pXiβi+ϵ其中: ϵ ∼ N ( 0 , σ 2 ) \epsilon \thicksim N(0,\sigma^2) ϵ∼N(0,σ2) 让我们聚焦众多参数中的一个:βi 。βi 的意义是什么呢?当其他变量保持不变,而只有 Xi 变动时,每变动一个单位的 Xi,就会让 Y 平均变动 βi 个单位。而若 Xi 的变动能够确确实实引起 Y 的变动, 那么 βi 应该不等于0。换句话说,若可以验证 βi 不为0,那么就可以证明Xi 与 Y 存在线性相关关系。 【注1】 这里的关系是线性的。二次即更高阶的相关性并不能由 βi 是否等于0体现; 【注2】 Xi 与 Y 存在相关关系,并不能证明二者之间存在 因果关系(Causality)。 然而,我们现在只有 βi 的估计量 β^OLS,i ,而估计量与参数的真实值有一定的误差。由于 β^OLS,i 是一个统计量,因此只要我们在统计意义下验证 βi 是否等于零就可以了。 至此,我们就可以构造一个如下的假设检验问题: H 0 : β i = 0 H 1 : β i ≠ 0 H_0: \beta_i=0 \\ H_1: \beta_i\ne0 H0:βi=0H1:βi=0 2.2 检验统计量——t统计量的构造若想构造检验统计量,我们需要先对 β^OLS,i 进行变型。 记矩阵 (XTX)-1 的对角线元素: diag ( X T X ) − 1 = ( v i , i ) p + 1 \text{diag}(\bm{X}^T \bm{X} )^{-1} = (v_{i,i})_{p+1} diag(XTX)−1=(vi,i)p+1 由第一部分中 β^OLS 服从的分布,我们可以得到 β^OLS,i 的分布: β ^ O L S , i ∼ N ( β i , σ 2 v i , i ) , i = 0 , 1 , . . . , p \hat\beta_{OLS, i} \thicksim N(\beta_i, \sigma^2 v_{i,i}) , \ i=0, 1,...,p β^OLS,i∼N(βi,σ2vi,i), i=0,1,...,p 将 β^OLS 标准化,有: β ^ O L S , i − β i σ v i , i ∼ N ( 0 , 1 ) , i = 0 , 1 , . . . , p \frac {\hat\beta_{OLS,i} - \beta_i}{ \sigma \sqrt{v_{i,i}} } \thicksim N(0, 1) , \ i=0, 1,...,p σvi,i β^OLS,i−βi∼N(0,1), i=0,1,...,p 然而,此时总体标准差σ 为未知参数,因此需要用样本标准差 σ^ 来代替。由于 σ^2OLS 有分布: ( N − P − 1 ) σ ^ O L S 2 σ 2 ∼ χ N − p − 1 2 \frac {(N-P-1) \hat \sigma _{OLS}^2} {\sigma^2} \thicksim \chi^2_{N-p-1} σ2(N−P−1)σ^OLS2∼χN−p−12 由 t 分布的定义: ( N − p − 1 ) ( β ^ O L S , i − β i ) σ v i , i / ( N − p − 1 ) σ ^ O L S 2 σ 2 = β ^ O L S , i − β i σ ^ v i , i ∼ t N − p − 1 \frac {\sqrt{(N-p-1)} (\hat\beta_{OLS,i} - \beta_i ) } { \sigma \sqrt{v_{i,i}} } / \sqrt{\frac {(N-p-1)\hat \sigma _{OLS}^2} {\sigma^2} } \\ =\frac {\hat\beta_{OLS,i} - \beta_i}{\hat \sigma \sqrt{v_{i,i}} } \thicksim t_{N-p-1} σvi,i (N−p−1) (β^OLS,i−βi)/σ2(N−p−1)σ^OLS2 =σ^vi,i β^OLS,i−βi∼tN−p−1 若原假设 H0 成立,即 βi = 0,可以定义 t 统计量(又称 t 值): t = β ^ O L S , i σ ^ v i , i ∼ t N − p − 1 t= \frac {\hat\beta_{OLS,i}}{\hat \sigma \sqrt{v_{i,i}} } \thicksim t_{N-p-1} t=σ^vi,i β^OLS,i∼tN−p−1 并称上式分母项为 β^OLS,i 的标准误(Standard Error, SE)。 从 t 统计量的定义式可以看出,t 的绝对值越大,β^OLS,i 越不等于0,原假设越有可能出错,我们越应该拒绝原假设。 注1:t 值的几何意义为 β^OLS,i 偏离其标准误的单位数; 注2:当N足够大时,t 统计量近似服从标准正态分布,因此可以使用标准正态分布进行替代。关于 t 分布与正态分布的关系,可参考文献[1] t分布收敛于标准正态分布的几种证明方法。 注3:关于t分布与t检验相关的更多知识,可参考文献[2] 我懒得找了。 2.3 拒绝域的构造然而,t 统计量多大算大呢?多大我们才应该拒绝原假设呢? 假设原假设 H0 正确,根据 t 统计量所对应的分布,在给定某一概率 1-α(我们称其为置信水平(Confidence Level))的前提下,t 统计量应该满足: P { ∣ t ∣ > t α 2 , N − p − 1 } < α P\{ |t| >t_{\frac{\alpha}{2}, N-p-1} \}< \alpha P{∣t∣>t2α,N−p−1} t0.025,N-p-1,我们就有足够的理由去认为原假设不正确,从而拒绝原假设。 基于这种思想,我们可以构造出一个区域(称为拒绝域(Rejection Field)): ( − ∞ , − t α 2 , N − p − 1 ) ∪ ( t α 2 , N − p − 1 , + ∞ ) (-\infin,-t_{\frac{\alpha}{2}, N-p-1}) \ \cup \ (t_{\frac{\alpha}{2}, N-p-1}, +\infin) (−∞,−t2α,N−p−1) ∪ (t2α,N−p−1,+∞)
当 t 统计量落入这个区域时,我们都应该拒绝原假设H0,并认为 βi 不等于0,自变量 Xi 与因变量 Y 存在统计意义下显著的线性相关关系(Statistically Significant Linear Correlation)。 注1:拒绝域,顾名思义,即若t值落入这个区间就应该拒绝原假设H0; 注2:在应用时,我们可以记住一句口诀:t值(的绝对值)越大越拒绝。 2.4 浅谈p值此外,许多统计软件在回归的结果中会给出参数估计量所对应的p值(p-value)。p值的意义是:拒绝原假设所需要的最小置信度。什么意思呢?就是说,如果给出的p值小于你需要的置信度 α ,那么我们就应该拒绝原假设。也就是说,若: p-value < α \text{p-value}F>Fα(p,N−p−1)} Fα(p, N - p - 1),我们就有足够的理由去认为原假设不正确,从而拒绝原假设。 基于这种思想,我们可以构造拒绝域:
(
F
α
(
p
,
N
−
p
−
1
)
,
+
∞
)
(F_\alpha(p, N-p-1), +\infin)
(Fα(p,N−p−1),+∞) 当 F 统计量落入拒绝域内时,我们应该拒绝原假设H0,从而认为模型是显著的,或者说解释变量 X 与被解释变量 Y 之间存在显著的线性相关关系。 4. 总结在这篇文章中,我们分别研究了单变量的显著性检验和模型的显著性检验。 (1)在单变量检验中,我们构造了假设检验问题: H 0 : β i = 0 H 1 : β i ≠ 0 H_0: \beta_i=0 \\ H_1: \beta_i\ne0 H0:βi=0H1:βi=0 构造了检验统计量—— t 统计量: t = β ^ O L S , i S E ( β ^ O L S , i ) ∼ t ( N − p − 1 ) t= \frac {\hat\beta_{OLS,i}}{SE(\hat \beta_{OLS,i})}\thicksim t(N-p-1) t=SE(β^OLS,i)β^OLS,i∼t(N−p−1) 并给出了拒绝域: ( − ∞ , − t α 2 ( N − p − 1 ) ) ∪ ( t α 2 ( N − p − 1 ) , + ∞ ) (-\infin,-t_\frac{\alpha}{2}(N-p-1)) \ \cup \ (t_\frac{\alpha}{2}(N-p-1), +\infin) (−∞,−t2α(N−p−1)) ∪ (t2α(N−p−1),+∞) (2)在模型检验中,我们构造了假设检验问题: H 0 : β 1 = β 2 = . . . = β p = 0 H 1 : ∃ i ∈ { 1 , 2 , . . . , p } , s . t . β i ≠ 0 H_0: \beta_1 = \beta_2 = ... = \beta_p =0 \\ H_1: \exist \ i \in \{1,2,...,p\}, s.t. \ \beta_i\ne0 H0:β1=β2=...=βp=0H1:∃ i∈{1,2,...,p},s.t. βi=0 构造了检验统计量—— F 统计量: F = E S S / p R S S / N − p − 1 ∼ F ( p , N − p − 1 ) F = \frac{ESS/p}{RSS/N-p-1} \thicksim F(p, N-p-1) F=RSS/N−p−1ESS/p∼F(p,N−p−1) 并给出了拒绝域: ( F α ( p , N − p − 1 ) , + ∞ ) (F_\alpha(p, N-p-1), +\infin) (Fα(p,N−p−1),+∞) 至此,我们解决了如何验证各个解释变量对因变量是否存在显著的线性影响,以及模型中涉及到的解释变量总体是否对因变量是否存在显著的线性影响。 参考文献[1] t分布收敛于标准正态分布的几种证明方法 写在最后欢迎感兴趣的小伙伴来跟作者一起挑刺儿~ 包括但不限于语言上的、排版上的和内容上的不足和疏漏~ 一起进步呀! 有任何问题,欢迎在本文下方留言,或者将问题发送至勘误邮箱: [email protected] 谢谢大家! |
【本文地址】
今日新闻 |
推荐新闻 |
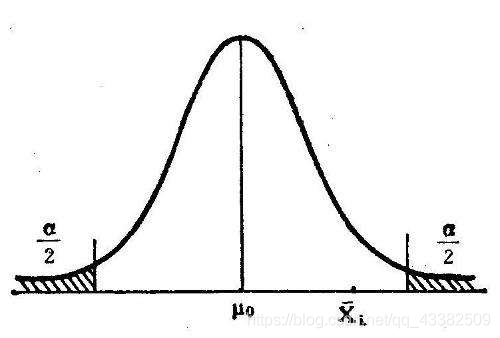 图1 t检验拒绝域构造示意图(阴影部分即为对应显著性水平下的拒绝域。图片来源:百度图片)
图1 t检验拒绝域构造示意图(阴影部分即为对应显著性水平下的拒绝域。图片来源:百度图片)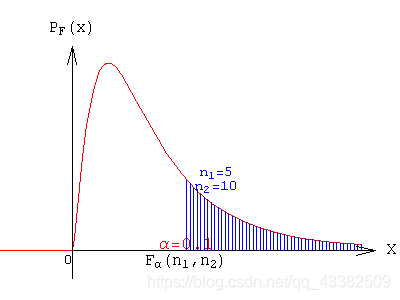 图2 F检验拒绝域构造示意图(阴影部分即为对应显著性水平下的拒绝域。图片来源:百度图片)
图2 F检验拒绝域构造示意图(阴影部分即为对应显著性水平下的拒绝域。图片来源:百度图片)